EC 编码和 LRC 编码
理解本文，读者将收获
- EC/LRC 编码的基本数学原理
- EC/LRC 编码的优势和缺点
- EC/LRC 编码成本和性能核算模型
以下内容超出本文范围
- 如何编写一个工业级的 EC 编解码库
技术背景和动机
在前些篇文章中，我们已经使用了很大篇幅去描述 “复制（增加数据冗余度）” 的重要性。
一种广泛应用且简单的复制方式即副本复制。然而副本复制存在一些问题，使我们不得不寻找更加灵活的编码方式去增加数据冗余度。
单纯使用副本复制，存在以下局限性：
- 只能以数据整数倍扩增，比如 1 副本、2 副本、3 副本等等。
- 一般经验上，结合硬件的故障率，至少需要使用 3 副本才能满足数据的安全性保证。
- 成本因此至少承担 3 倍数据的存储、写带宽。
实际上不是所有的数据都值得使用 3 倍冗余去储存。梳理下就会发现，根本的技术障碍为：整数倍的冗余。
一旦能够打破这个限制，我们能够根据实际的硬件损坏概率，灵活地安排冗余度/成本/性能的平衡。
因此实际的技术需求变为：我们需要一种编码方式，能够
- 灵活安排数据和冗余的配比
- 冗余信息熵逼近故障容忍所需的熵增量
- 计算相对快速
- 易于理解和控制
Erasure Code (EC) 因符合上述需求，被分布式存储广泛使用。
Head First EC
关于 EC 编码的简明数学原理和工程经验，可参考 OpenACID Blog 优秀的 EC 系列文章123。笔者强烈建议读者抽时间理解 EC 的数学原理。本文则从系统设计角度出发，考虑 EC 的使用手法，假设读者可以直接使用成熟的编码库，如 isa-l4 等。
EC 编解码：input / output
感性上，我们可将 EC 编解码器想象成一个神奇的黑魔法模块。正常情况下，我们可以输入数据块，得到一些校验块。
不妨想象一个 4MiB 的数据。由于内部是矩阵计算，我们需要确定这次编码的块的长度，不妨定为 1MiB。则我们得到 [D1, D2, D3, D4] 共 4 份，每份长度为 1MiB 的数据块。
我们也可以决定要输出多少个校验块出来，不妨设为 2 块。则编码器输出 [P1, P2] 共 2 份，每份长度为 1MiB 的校验块。
最终得到的块序列为 [D1, D2, D3, D4, P1, P2]。我们记为 EC(4,2)。
总结下，我们可控的 EC 编码器的参数为
- 块的长度：单个数据块的长度 B
- 数据块数量：m
- 校验块数量：n
则编码器的输入输出如下：
- 编码输入为： m 个 长度为 B 的数据块
- 编码输出为：n 个 长度为 B 的校验块
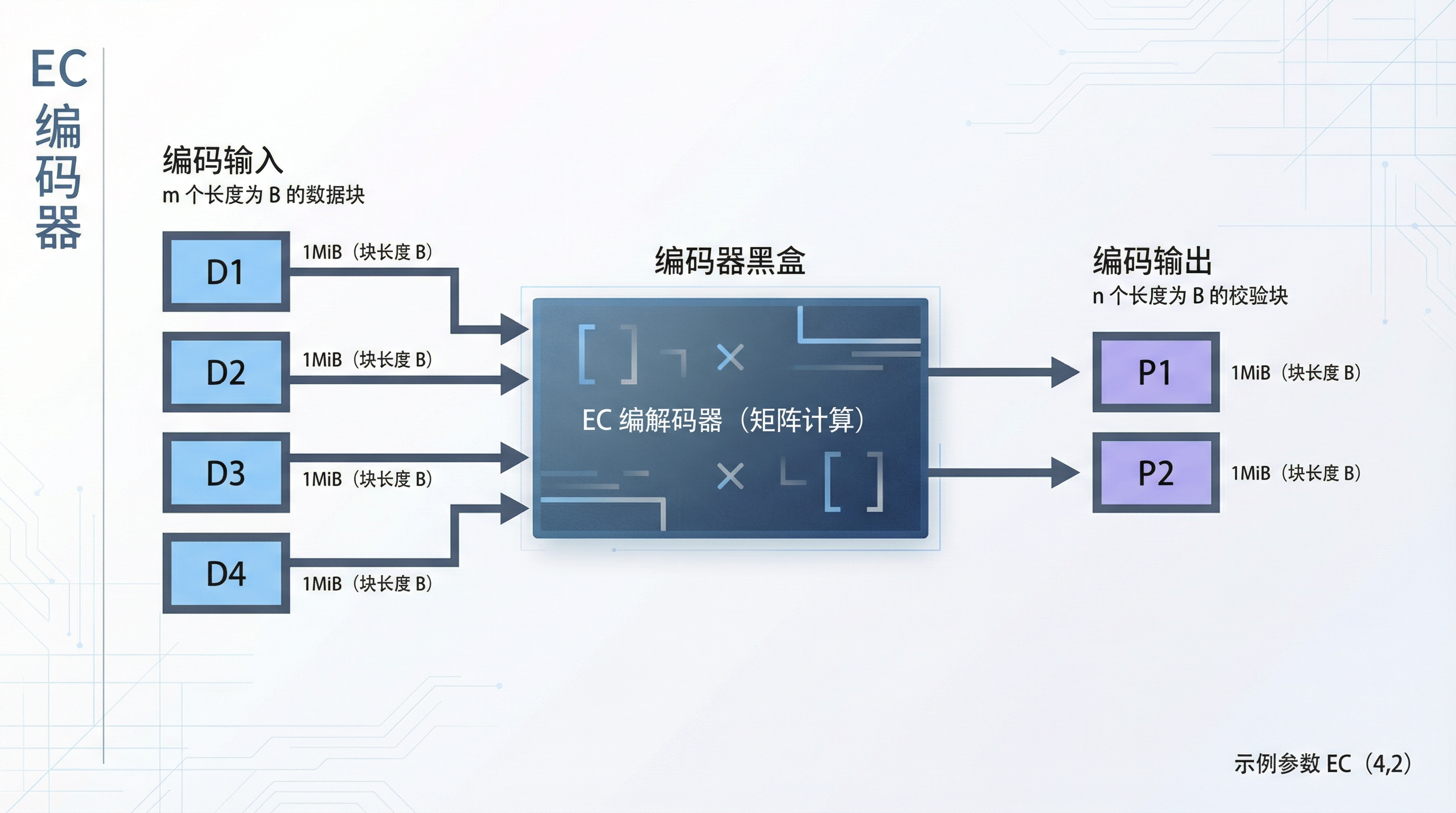图： EC 的编码器
别忘了 EC 的目的是冗余和数据修复。我们因故缺失了一些数据块，则需要解码器修复原始数据。
对于我们上述的 EC(4，2)，设序列为 [D1, D2, D3, D4, P1, P2]。假设丢失了 D1 和 D4，则可根据 [D2, D3, P1, P2] 解出 [D1, D4]。
图： EC 的解码器
冗余度和信息论
数据组织：stripe / one-by-one
性能模型
成本模型
数据安全性模型
集群修复速度
MTTR